- Home
- right triangle with
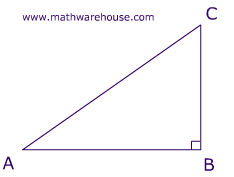
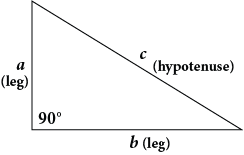
- How do you use the Pythagorean Theorem to determine if the following triangle with sides a, b, & c is a right triangle: a=5, b=10, c=15?
How do you use the Pythagorean Theorem to determine if the following triangle with sides a, b, & c is a right triangle: a=5, b=10, c=15?
5 (294) · $ 23.50 · In stock
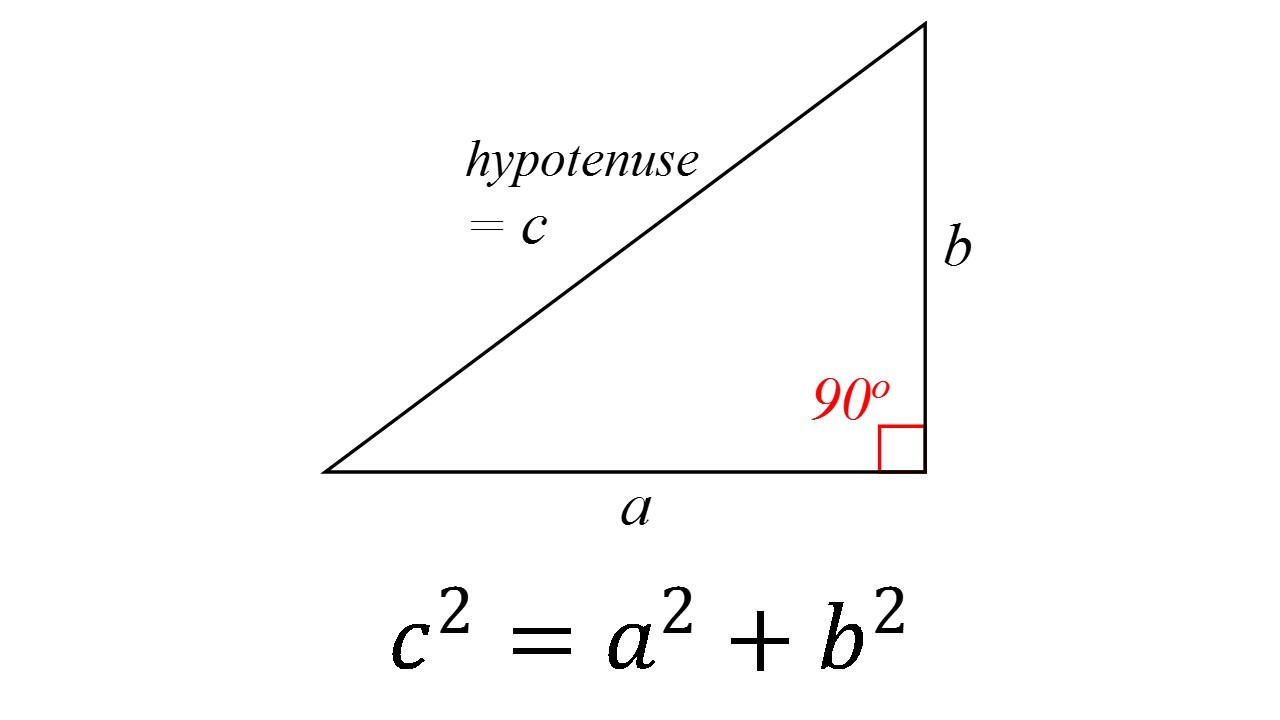
c^2 != a^2 + b^2, therefore, this cannot be a right triangle. The Pythagorean Theorem applies to right angle triangles, where the sides a and b are those which intersect at right angle. The third side, the hypotenuse, is then c To test whether the given lengths of sides create a right triangle, we need to substitute them into the Pythagorean Theorem - if it works out then it is a right angle triangle: c^2 = a^2 + b^2 15^2 != 5^2+10^2 225 != 25+100 225 != 125 In reality, if a=5 and b=10 then c would have to be c^2 = 125 c =sqrt(125) = 5sqrt(5)~= 11.2 which is smaller than the proposed value in the question. Therefore, this cannot be a right triangle.
How to Calculate the Sides and Angles of Triangles Using

Pythagorean Theorem Formula, Derivation, and solved examples

4.27: The Pythagorean Theorem - K12 LibreTexts

Lesson 7-2 Lesson 7-2: The Pythagorean Theorem1 The Pythagorean

How to Determine Whether a Triangle is a RIGHT Triangle
In a right triangle the length of the hypotenuse is 10 cm and the
What is the Pythagorean theorem, and how is it used to solve

Non-right Triangles: Law of Cosines
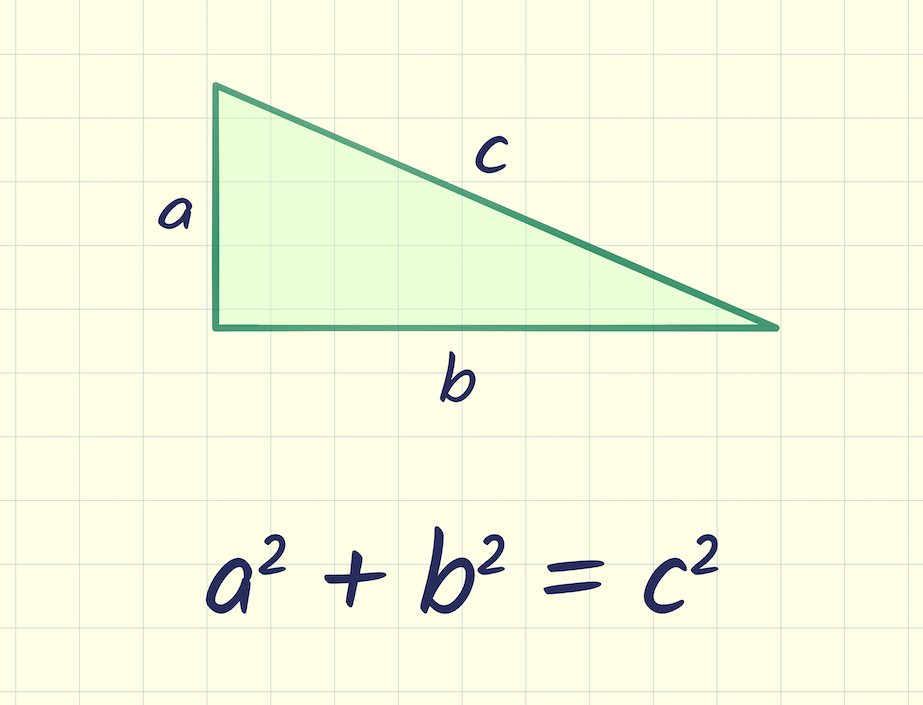
Why the Pythagorean Theorem Is True, by Slawomir Chodnicki

1. Given: Triangle ABC with vertices A,B,C. Prove: Triangle ABC is




/product/82/587144/1.jpg?2712)